homestaya.blogg.se - Quadratic programming

Pardalos (eds.): Recent Advances in Global Optimization, Princeton Univ.

Vavasis, S.A.: ‘On approximation algorithms for concave quadratic programming’, in C.A. Vavasis, S.A.: ‘Local minima for indefinite quadratic knapsack problems’, Math. Vavasis, S.A.: ‘Approximation algorithms for indefinite quadratic programming’, Math. Vavasis, S.A.: Nonlinear optimization: Complexity issues, Oxford Univ. Vavasis, S.A.: ‘Quadratic programming is in NP’, Inform. Tardos, E.: ‘A strongly polynomial algorithm to solve combinatorial linear programs’, Oper. Sahni, S.: ‘Computationally related problems’, SIAM J. Renegar, J.: ‘A polynomial-time algorithm based on Newton’s method for linear programming’, Math. Pardalos, P.M., and Vavasis, S.A.: ‘Quadratic programming with one negative eigenvalue is NP-hard’, J. Pardalos, P.M., Han, C., and Ye, Y.: ‘Algorithms for the solution of quadratic knapsack problems’, Linear Alg. Nemirovsky, A.S., and Yudin, D.B.: Problem complexity and method efficiency in optimization, Wiley, 1983. Murty, K.G., and Kabadi, S.N.: ‘Some NP-complete problems in quadratic and nonlinear programming’, Math. , and Straus, E.G.: ‘Maxima for graphs and a new proof of a theorem of Turán’, Canad. Moré, J.J., and Vavasis, S.A.: ‘On the solution of concave knapsack problems’, Math. Megiddo, N.: ‘Linear programming in linear time when the dimension is fixed’, J. Kozlov, M.K., Tarasov, S.P., and Hačijan, L.G.: ‘Polynomial solvability of convex quadratic programming’, Soviet Math. Karmarkar, N.: ‘An interior-point approach to NP-complete problems’, Preprint (1989).

Karmarkar, N.: ‘A new polynomial-time algorithm for linear programming’, Combinatorica 4 (1984), 373–395. Kapoor, S., and Vaidya, P.M.: ‘Fast algorithms for convex quadratic programming and multicommodity flows’: Proc. Helgason, R., Kennington, J., and Lall, H.: ‘A polynomially bounded algorithm for a singly constrained quadratic program’, Math. Hačijan, L.G.: ‘A polynomial algorithm in linear programming’, Soviet Math. 2 (1995), 488–499.įu, M., Luo, Z.-Q., and Ye, Y.: ‘Approximation algorithms for quadratic programming’, Working Paper Dept. 61 (1993), 39–52.Ĭlarkson, K.L.: ‘Las Vegas algorithms for linear and integer programming when the dimension is small’, J. SeeComplexity theory: Quadratic programmingellipsoid methodĪdler, I., and Shamir, R.: ‘A randomization scheme for speeding up algorithms for linear and convex quadratic programming problems with a high constraints-to-variables ratio’, Math.SeeComplexity theory: Quadratic programmingbox constraints.SeeComplexity theory: Quadratic programmingsimplicial constraints.SeeComplexity theory: Quadratic programming Cutting-stock problem Simplicial pivoting algorithms for integer programmingknapsack problem.

SeeComplexity theory: Quadratic programmingstrongly polynomial time.

SeeComplexity theory: Quadratic programmingtrust region problem.

SeeComplexity theory: Quadratic programminglocal minimization.

SeeComplexity theory: Quadratic programming Frank–Wolfe algorithm Linear complementarity problem Operations research and financial markets Portfolio selection: Markowitz mean-variance model Quadratic knapsack Quadratic programming over an ellipsoid Quadratic programming with bound constraints Replicator dynamics in combinatorial optimization Sensitivity and stability in NLP: Approximation Successive quadratic programming: Solution by active sets and interior point methodsquadratic programming.

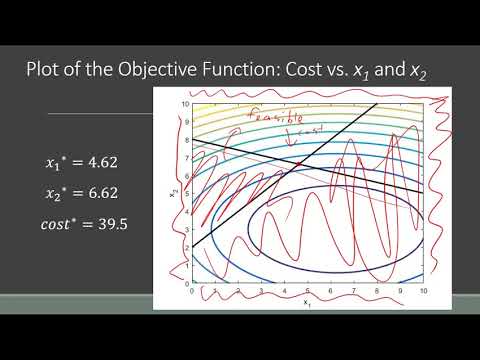
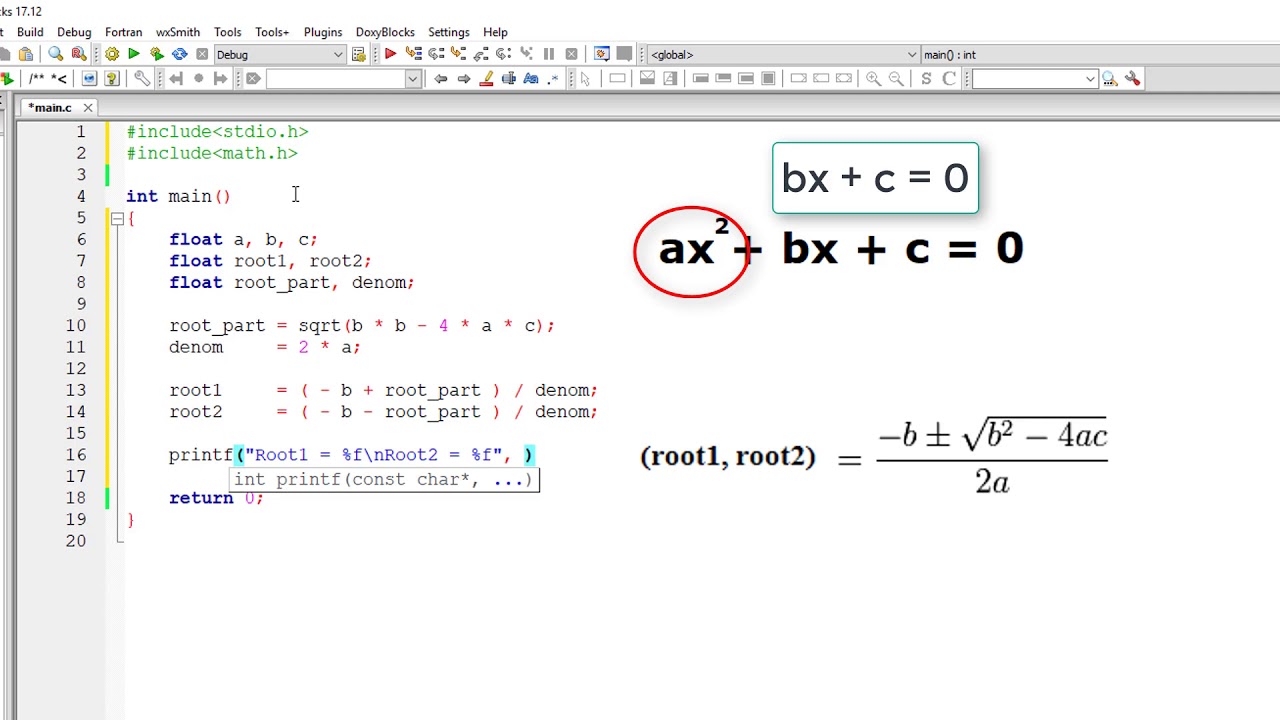
In particular, there is no local minimizer other. Convex quadratic programming inherits all the desirable attributes of the general convex programming.